线性回归的从零开始实现

参考：《动手学深度学习》
通过利用mxnet框架中的NDArray和autograd来实现一个线性回归的训练过程

导入所需要的包

1
2
3
4
5
%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random

生成数据集

我们设定有两个特征值x1， x2，回归模型真实值为y = 2x1 - 3.4x2 + 4.2
其中w1 = 2, w2 = -3.4, b = 4.2
加入一个随机噪声∈来生成标签label，即y = 2x1 - 3.4x2 + 4.2 + ∈
∈符合均值为0，标准差为0.01的正态分布

1
2
3
4
5
6
7
8
9
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
#随机生成特征值
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
#根据特征值得到标签值
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
1
features[0], labels[0]
(
 [0.5086958  0.91511744]
 <NDArray 2 @cpu(0)>,

 [2.0881135]
 <NDArray 1 @cpu(0)>)
1
2
3
4
5
6
7
8
9
10
11
12
13
def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize

set_figsize()
#把features与label的对应关系展示出来
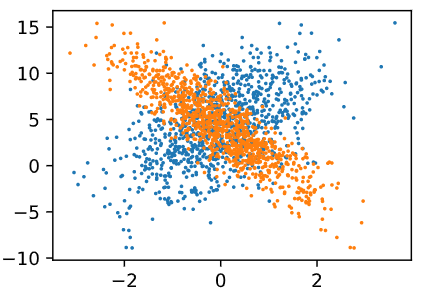
plt.scatter(features[:, 0].asnumpy(), labels.asnumpy(), 1)
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1)
<matplotlib.collections.PathCollection at 0x7fda87eb0c88>

​

读取数据集

1
2
3
4
5
6
7
8
9
#从features中读取数据，我们每次读取batch_size个数据，
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) #读取是随机的
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])
        yield features.take(j), labels.take(j)
    
1
2
3
4
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break #只输出一组batch_size，没有break将会输出所有的
[[ 0.01437022 -2.3105397 ]
 [-0.1742568   0.65264654]
 [ 1.2812718  -0.96987015]
 [-0.2819217  -0.24931197]
 [-0.11592119  0.0309534 ]
 [ 0.60624367  0.76104844]
 [-1.0258828   0.6976225 ]
 [-1.779809    0.5851231 ]
 [ 1.4180893  -0.62011564]
 [-0.87209934  0.6670822 ]]
<NDArray 10x2 @cpu(0)> 
[12.096044    1.6319575  10.049137    4.503763    3.8513668   2.8237865
 -0.23646423 -1.3559463   9.153078    0.19797151]
<NDArray 10 @cpu(0)>

初始化模型参数

1
2
3
4
5
6
#权重初始化,权重初始化成均值为0，标准差为0.01的正太随机数
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))
#创建梯度
w.attach_grad()
b.attach_grad()

定义模型、损失函数、优化算法

1
2
3
4
5
6
7
8
9
10
#定义线性模型模型
def linreg(X, w, b):
    return nd.dot(X, w) + b
#损失函数
def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
#定义优化算法
def sgd(params, lr, batch_size):  # 本函数已保存在d2lzh包中方便以后使用
    for param in params:
        param[:] = param - lr * param.grad / batch_size

训练模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#训练模型
#其中学习率lr为0.03，迭代次数num_epochs
lr = 0.03
num_epochs = 5
net = linreg
loss = squared_loss

for epoch in range(num_epochs): 
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y)  # l是有关小批量X和y的损失
        l.backward()  # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))
epoch 1, loss 0.000050
epoch 2, loss 0.000050
epoch 3, loss 0.000050
epoch 4, loss 0.000050
epoch 5, loss 0.000050

把学习得到的参数与真实参数对比

1
true_w, w
([2, -3.4],

 [[ 2.0009615]
  [-3.400259 ]]
 <NDArray 2x1 @cpu(0)>)
1
true_b, b
(4.2,

 [4.2000113]
 <NDArray 1 @cpu(0)>)